2° Exame de qualificação da Uerj - 2014

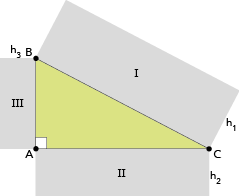
Na figura a seguir, estão representados o triângulo retângulo ABC e os retângulos semelhantes I, II e III, de alturas h₁, h₂ e h₃ respectivamente proporcionais às bases 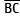 ,  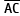e .

  

Se  = 4 m e  = 3 m, a razão  é igual a:

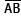(A) 5

(B) 4

(C) 3

(D) 2

Resolução:

Como o triângulo ABC é retângulo em A, podemos aplicar o Teorema de Pitágoras para encontrar a hipotenusa BC (lembre que a hipotenusa sempre será o lado oposto ao ângulo reto).

Teorema de Pitágoras

(hipotenusa)² = (cateto 1)² + (cateto 2)²

dados:
hipotenusa = lado BC

cateto 1 = lado AB = 3 m

cateto 2 = lado AC = 4 m

Aplicando no teorema, teremos:

BC² = 3² + 4²

BC² = 9 + 16

BC² = 25   (aplicando raiz quadrada nos dois membros...)

BC = 5   

Como no enunciado diz que h1, h2 e h3 são proporcionais a BC, AC e AB, temos que:

Sendo k a constante de proporção.

Agora vamos aplicar na razão pedida:

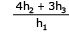
Resposta: Letra (A)

Nível: Médio

62,07% dos candidatos acertaram a questão

Conceitos: 

* Teorema de Pitágoras

* Proporção